Lassan eltelt egy hónap 2025-ből és még mindig nem tartottam évértékelőt 2024 kapcsán. Nem mintha korábban tartottam volna ilyet, de ahogy érzékelem a médiából, számos szereplőnél ez februárban válik időszerűvé. A tavalyi év abban a tekintetben volt különleges számomra, hogy 2024 januárban kitöltöttem a Mélylevegő projekt Évtervezőjét. Az év folyamán ezt nem vettem elő, de végig a fejemben volt, hogy milyen irányokat szabtam magamnak a barátok, a család, a párkapcsolat, a munka és a szabadidő kapcsán. Utólag visszanézve nem úgy alakult, ahogy elterveztem és ennek kapcsán van is bennem rossz szájíz. Mindez azonban eltörpül amellett, hogy ha összességében nézem a tavalyi évet, akkor azt tudom mondani, hogy nagyon is jó volt.
Jó volt, mert rólam szólt. Mert azokon az eseményeken vettem részt, ahol akartam (pl. olimpia Párizsban, fesztivál Máltán, szörfözés a Kanári-szigeteken), de nem feltétlenül azokkal, akikkel akartam. A 2024-es repüléseim tükrében elmondhatom, hogy eljutottam arra a pontra, hogy már fontosabb az, hogy kivel utazom, mint az, hogy hova. Egy évvel korábban nem így gondoltam, akkor még fontosabb volt, hogy utazzak és hogy ezt minél jobb kondíciókkal (olcsó repülőjegy, olcsó szállás, jó éttermek, jó programok, izgalmas környezet) tegyem meg.

A rövid távú céljaim teljesültek, de a hosszabb távú céljaimhoz nem kerültem közelebb. Nem adtam fel, de nem is görcsöltem rá a mindennapokban. Más kérdés, hogy saját személyiségfejlődésem tükrében úgy vélem, hogy valójában ez a legnehezebb feladat az életben; ám erre a pontra is el kellett jutni. És amikor mások erre évközben rávilágítottak, nos, nagyon nem akartam azonosulni vele. Hogy dacból-e, azt nem tudom, de épp ennyi idő kellett, hogy ebben a témában is felnőjek.
Apropó nehézség, ennek kapcsán ugrott be egy videó, amin Orosz László, egy azóta elhunyt BME-s tanár osztotta meg gondolatait a természet és a matematika kapcsán. Arra világított rá, hogy a matematika rendkívül jól képes leírni a természet törvényeit, de hogy ez miért működik, arra csak a filozófusok tudják a választ. Nagyon szeretem Orosz tanár úr előadásait nézni; még akkor is, ha alig értek valamit a kvantummechanikából.

Ám az előadásai elején és közben rendszeresen tartott eszmefuttatásokat, amik nagyon szenvedélyesek. A bölcsessége, történelmi tapasztalata, komplex világnézete rendkívül jó előadói képességekkel párosult. Elég ha a gondolkodás nehézségei vagy a lényeges és lényegtelen dolgok közötti különbségtétel kapcsán megfogalmazott szösszenetekre gondolunk. Hogy tanárként milyen volt, azt nem tudom, az én véleményem pusztán ezen videókon alapul.
A lényeg, hogy a feladatok nehézsége és az egyik videó kapcsán született néhány ötletem bizonyos görbék kapcsán. Görbék, amely az élet valamilyen vagy akár több területéhez kötődnek és pusztán gyakorlati tapasztalataim alapján azt állítom, hogy jellegükben jól leírják a folyamatokat. Nevezzük ezeket a görbéket moneytime-görbéknek vagy akár moneytime-törvényeknek a mögöttes folyamatokat. Ha a reprezentatív felmérések, vizsgálatok is igazolják majd a feltételezésem, akkor ígérem, a nevemre veszem ezeket.
Moneytime első törvénye alapján minél előrébb tartunk egy feladatban, egy projektben; annál kisebb haladást lehet elérni egységnyi erőfeszítéssel. Matematikailag szerintem a négyzetgyök(x) függvénnyel érdemes leírni, magát a függvényt pedig a lenti ábra szemlélteti. Mit is jelent ez a mindennapokban és hogyan hasznosítható a gondolatmenet? Az ötlet legelőször egy prezentáció kapcsán merült fel, azután rendre felbukkant egy elemzés, egy előadás kapcsán is.
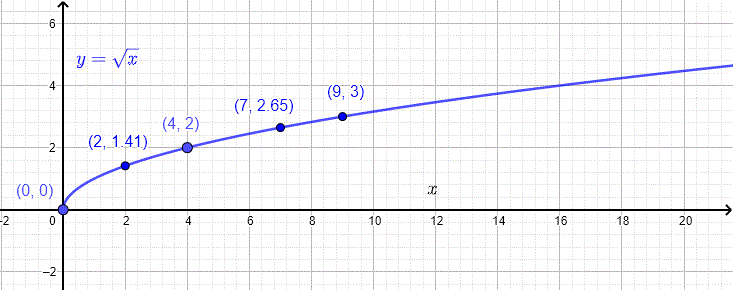
A grafikon azt szemlélteti, hogy pl. nulláról indulva nagyon gyorsan el lehet érni egy 50-60%-os vagy akár egy 80%-os stádiumot egy feladatban, egy projektben. Amikor még üres a PPT, amikor még csak elkezdünk megkutatni egy pénzügyi eszközt, egy politikai, egy szociológiai kérdést, akkor rendkívül erőforrásigényes a projekt.
Ha a fenti grafikon tükrözi egy teljes projekt státuszát, akkor pl. 5 embernap alatt jutunk el 50%-os állapotba. A következő 5 embernap felhasználásával viszont kisebb előrelépést tudunk felmutatni, mert az csak 80%-os stádiumba visz el minket elméletben. És egy további embernap pedig 90%-os szintre visz el. A folyamat a mikroökonómiából a csökkenő határhaszon elméletével cseng össze, azzal a különbséggel, hogy itt nincs negatív mozgás.
A lényeg, hogy vezetőként vagy csapattagként mindig azt érdemes mérlegelni, hogy milyen mélységben szükséges bemutatni az adott témát az adott közönségnek. Mert a legtöbbször elég a 80% is, sőt néha időprésben az 50% is bőven felülteljesítésnek tűnik. Ez a gondolat nem tűnik nagy truvájnak, viszont nekem, aki alapvetően maximalista közegben cseperedett fel, óriási dilemmát jelentett a szerintem félkész vagy fércmunkák kiadása a kezemből. Holott már egy kis szervezet is értékeli, ha a csapattagok ilyen szemüveggel dolgoznak.

Az elmúlt években fokozatosan hozzászoktam ehhez a grafikonhoz a munkám során; és egyre gyakorlottabb vagyok abban, hogy egy kapott vagy kreált feladatnál körvonalazzam a várható mélységét. A sors fintora, hogy vezetői karrierem során számos kollégám volt, aki szintén maximalista közegben szocializálódott és most már megértem és tudom fogni a kezüket, hogy ők is megértsék ezt a szemléletet. Mert ha egy feladatot 80%-on végzünk el és a fennmaradó időben másik feladatot pipáltunk, akkor gyakran több értéket teremtettünk és hasznosabban voltunk az ügyfeleknek és a szervezetnek.
Persze ez a szemlélet nem csak a munka világában jelenik meg, a mindennapokban is használható. Egy vizsgára készülés vagy éppen egy randevú, egy üzleti ebéd során nagyon gyorsan el tud mélyülni a kapcsolat egy bizonyos szintig, de egy tartós kapocs kialakításához lényegesen több idő kell. Az egyik barátom, István mesélte nemrég, hogy még 8 év házasság után is meg tudta lepni őt a felesége – jó értelemben –, azaz még akkor is felfelé ívelt kapcsolatuk. Azaz sokkal több volt benne, mint amire korábban számítottak. Nyilván egy kapcsolatban alapvetően nem ilyen jellegűek a határidők mint a munkában, de mégis érdekes volt a párhuzam. És hogy mire érdemes még számítani? Moneytime második törvényéből kiderül hamarosan.






akoskuti hozzászólásai